

The efficiency of parallel computations depends on four factors: the distribution of computations among different processors, the processing speed of each processor, the amount of data that must be transmitted between different processors, and the speed of data communication between different processors. Fortunately, the emergence of message passing interface (MPI) and a number of libraries handling data communications between different processors, computers, or clusters of computers hide the complexity of hardware configurations from the implementation of parallel computations. Parallel computations intrinsically depend on the hardware configurations, shared memory, or distributed memory, etc. Routh, in Matrix Algorithms in MATLAB, 2016 5.7.2 Parallel Computationsīecause of the need to solve very large scale of sparse linear equation systems, parallel computations are becoming increasingly important. The answers check.Ħ00 adult tickets and 200 child tickets were sold.Ong U. Substitute 200 in for c in one of the original equations.Ĭ = 200 into the original system.
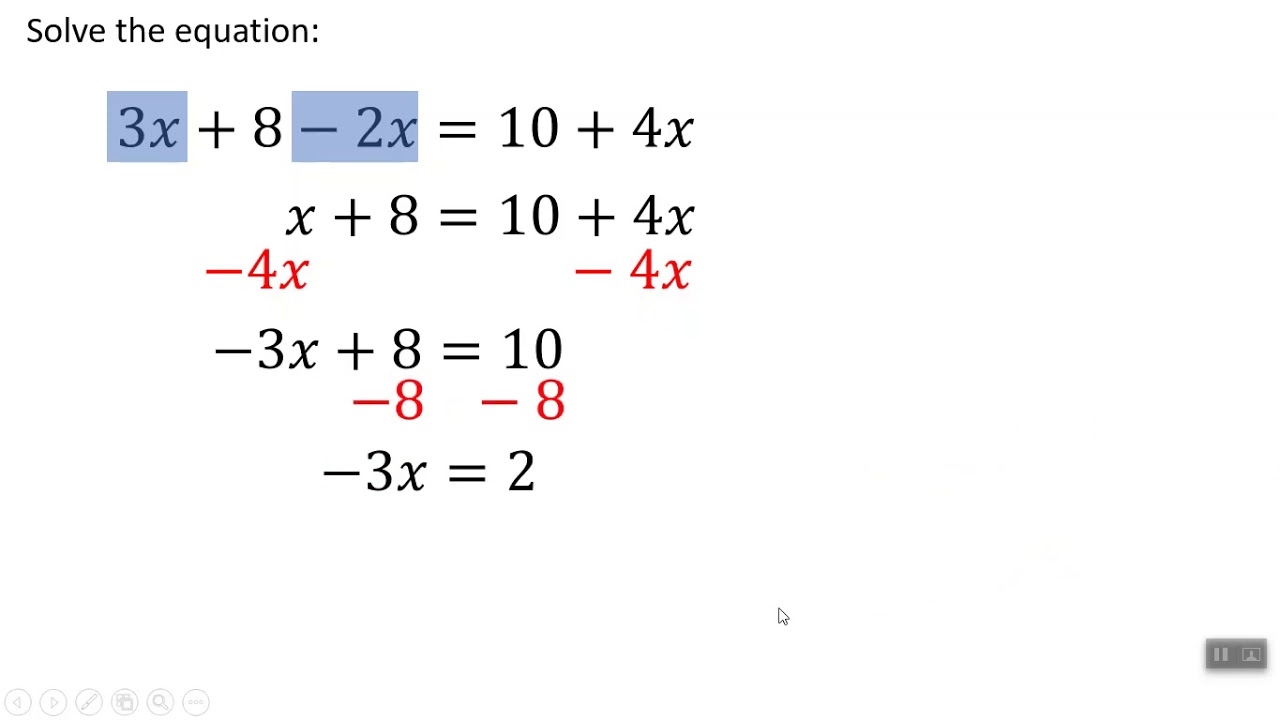
Use multiplication to re-write the first equation.Īdd the opposite of the second equation to eliminate a term and solve for c. Write a system of equations to model the ticket sale situation. How many of each type of ticket were sold? One child ticket costs $4.50 and one adult ticket costs $6.00.The total amount collected was $4,500. The correct answer is to add Equation A and Equation B.Ī theater sold 800 tickets for Friday night’s performance. Felix may notice that now both equations have a term of − 4 x, but adding them would not eliminate them, it would give you a − 8 x. Multiplying Equation B by − 1 yields − 3 y – 4 x = − 25, which does not help you eliminate any of the variables in the system. The correct answer is to add Equation A and Equation B. Instead, it would create another equation where both variables are present. Felix may notice that now both equations have a constant of 25, but subtracting one from another is not an efficient way of solving this problem. Multiplying Equation A by 5 yields 35 y − 20 x = 25, which does not help you eliminate any of the variables in the system. Adding 4 x to both sides of Equation A will not change the value of the equation, but it will not help eliminate either of the variables-you will end up with the rewritten equation 7 y = 5 + 4 x. Felix will then easily be able to solve for y. If Felix adds the two equations, the terms 4 x and − 4 x will cancel out, leaving 10 y = 30. If you multiply the second equation by −4, when you add both equations the y variables will add up to 0.ģ x + 4 y = 52 → 3 x + 4 y = 52 → 3 x + 4 y = 52ĥ x + y = 30 → − 4(5 x + y) = − 4(30) → − 20 x – 4 y = − 120Ĭorrect.

Notice that the first equation contains the term 4 y, and the second equation contains the term y. This is where multiplication comes in handy. You can multiply both sides of one of the equations by a number that will result in the coefficient of one of the variables being the opposite of the same variable in the other equation. So let’s now use the multiplication property of equality first. If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. Many times adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Using Multiplication and Addition to Eliminate a Variables


 0 kommentar(er)
0 kommentar(er)
